Vorschlag zur Verbesserung tabellarischer Längen- angaben von Höhlen Von Fritz Reinboth (Braunschweig)
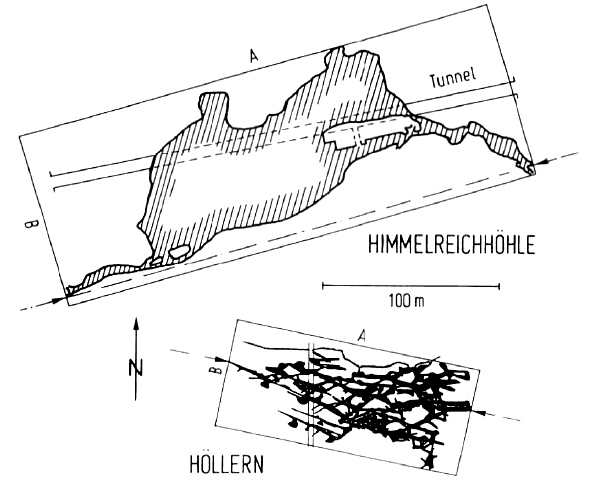
Die Aussage der „Gesamtganglänge“ (GGL) einer Höhle über ihre wissenschaftliche Bedeutung ist trotz einer eigens zur Aufstellung von vergleichenden Listen gebildeten UIS-Kommission seit jeher umstritten. Berühmte archäologische Höhlenfunde entstammen oft Kleinhöhlen oder Abris; eine Was sagen nun diese Zahlen? Es gibt seit langem Regeln, nach denen die jeweiligen Gesamtganglängen zu ermitteln sind (TRIMMEL 1968: 239), sodaß die Korrelierbarkeit der Daten gewährleistet zu sein scheint; daß es oft durchaus im Ermessen des Auswertenden liegt, welche Ausbuchtungen eines Höhlenganges er berücksichtigt, sei hier vernachlässigt. Auch ohne diese Einschränkung lassen sich Zweifel am Aussagewert der sogenannten Gesamtganglänge über die wirkliche Größe einer Höhle schnell verdeutlichen. Ein Vergleich der Grundrisse der mit 1040 m Gesamtlänge zu den Großhöhlen zählenden „Höllern“ im fränkischen Grundgips (GÖTZ, 1979) und der Himmelreichhöhle bei Walkenried im Harz, die mit 580 m geführt wird (REINBOTH 1970), verdeutlicht beispielhaft die Unsinnigkeit dieser Zahlenspiele (Abb. 1). Die ganze Höllern paßt etwa zweimal in den Grundriß der Haupthalle der Himmelreichhöhle, die zur Gesamtlänge ganze 170 Meter beisteuert! Ein Vergleich der Volumina wurde die Kriechgänge der Höllern gegen die weiträumige Himmelreichhöhle gänzlich in Bedeutungslosigkeit untergehen lassen. Man täte der morphologisch so bemerkenswerten Höllern bitter Unrecht, wenn man ihre Bedeutung durch ihr Volumen ausdrücken wollte; jedoch ist die Länge dafür ebensowenig signifikant.
Die Kluterthöhle, früher als „größte“ (korrekter wäre „längste“) deutsche Höhle geführt (GRIEPENBURG 1931: 56), hatte mit über 5 km Länge die Heimkehle bei Uftrungen als Schauhöhlenkonkurrenz mit eben 1780m Länge glatt aus dem Feld geschlagen. Die Heimkehle konterte mit der Feststellung, sie sei zwar nicht die längste, aber doch die volumenmäßig größte Höhle Deutschlands. Wie man aus diesem Beispiel ersieht, können solche „Rekordlängen“ auch kommerzielle Hintergründe haben. Damit wird wohl hinreichend deutlich, daß die Größe derart unterschiedlicher Höhlentypen sich eben nicht auf eine auch nur für bescheidenste Ansprüche aussagekräftige „Gesamtganglänge“ reduzieren läßt. Die wirkliche Größe einer Höhle wäre wohl am eindeutigsten durch ihr Hohlraumvolumen charakterisiert. In der Praxis stößt eine auch mir einigermaßen zuverlässige Angabe trotz des Computerzeitalters auf unüberwindliche Schwierigkeiten. Einfacher zu ermitteln und fast ebenso aussagekräftig ist die Grundfläche. Mit einem Planimeter ist sie auf einem Grundriß meistens schneller bestimmt als die Gesamtlänge. Da heute sehr viele Pläne auf dem Computer erstellt werden, ließe sich auch damit die Grundfläche einer Höhle errechnen. Ein einfaches, jedoch sehr mühseliges Verfahren wäre das Auszählen eines übergelegten maßstäblichen Rasters bzw. transparenten Millimeterpapiers. Bei Labyrinthhöhlen wie der ukrainischen Optimisticeskaja wird die Flächenbestimmung immer äußerst mühsam bleiben. Es muß also nach einer einfacheren Lösung gesucht werden, aus möglichst wenigen Zahlen eine repräsentative Aussage zu gewinnen. Dafür gibt es mehrere Möglichkeiten. Längenbezogene Gangdichte Neben der Gesamtlänge bietet sich als weitere Kenngröße einer Höhle der Abstand ihrer am weitesten voneinander entfernten Punkte an, den ich hier als ihre größte Ausdehnung Amax definiere (Beispiele in Abb. 1). Der Quotient dieser Längen ist die „längenbezogene Gangdichte“ Anschaulich sagt diese Kenngröße, wieviel Meter der Gesmtganglänge auf jeden Meter des Höhlenareals, in der Richtung seiner größten Ausdehnung gemessen, entfallen. Sie wird umso größer, je labyrinthischer oder mäandrierender ein Höhlensvstem wird und liefert somit eine einfach zu gewinnende zahlenmäßige Aussage über den Grundrißtyp einer Höhle. Die Aussage ist leider unabhängig von der lateralen Ausdehnung des Höhlensystems. Infolgedessen hat z. B. ein langgestreckter enger Gang und ein großer Einzelhohlraum die gleiche, gegen 12 gehende längenbezogene Gangdichte. Flächen- und volumenbezogene Gangdichte als weitere Möglichkeiten der Kennzeichnung des Grundrißtyps einer Höhle Günstiger ist es, die Gesamtganglänge auf die Fläche eines Rechtecks oder das Volumen eines Quaders zu beziehen, innerhalb dessen sich die Höhle ausdehnt und das mit zur Achse der größten Längenausdehnung parallelen bzw. orthogonalen Seiten oder Kanten eindeutig definiert ist (Beispiele in Abb. 1). Hier sei nur die flächenbzogene Gangdichte näher betrachtet. Bei der Quotientenbildung aus Länge und Fläche erhält man bei geometrisch ähnlichen Grundrissen verschiedener Größe unterschiedliche Zahlenwerte (noch krasser bei der Relation Länge/Volumen). Ein einfaches Beispiel mag das verdeutlichen: eine rechteckige Halle mit gleichem Seitenverhältnis sollte unabhängig von ihrer Größe natürlich den gleichen Kennwert haben. Für einen 10 m x 100 m großen Raum mit der GGL 100 m würde sich beispielsweise ergeben: G = 100 m/(10m x 100m) = 0.1 m/m²; für einen Raum mit gleichem Seitenverhältnis, aber nur 1 m x 10 in Größe dagegen nur G = 10 m/ (1m x 10m) = 1 m/m². Diese Vorgehensweise ist also für eine Kennzeichnung unbrauchbar. Die mißliche Quotientenbildung aus einer Länge und einer Fläche (oder eines Volumens) läßt sich vermeiden, indem alle Längen normiert, d. h. hier als Bruchteile der Gesamganglänge GGL ausgedrückt und somit dimensionslos gemacht werden. Allgemein gilt für diese Rechnung mit normierten Größen:
Darin ist Amax die größte Ausdehnung, Bmax die Breite der rechteckigen Bezugsfläche und Die Kenngröße GF sagt also, wie oft die Fläche des Rechtecks Amax x Bmax, in das eine Höhle einbeschrieben ist, in einem Quadrat mit der Seitenlänge GGL enthalten ist. Nach dieser Normierung ergibt sich jetzt für den ersten Fall (Normierung mit GGL = 100 m): GF = 1 / (0.1 x 1) = 10; für den zweiten Fall (Normierung mit GGL = 10 m) ergibt sich das Gleiche. Nur eine Halle mit gleicher Länge und Breite hat die flächenbezogene Gangdichte GF = 1. Die flächenbezogene Gangdichte spiegelt also auch die Gangbreite bzw. die laterale Ausdehnung eines Systems wider. Beispiele: Himmelreichhöhle (nach REINBOTH 1970), große Halle mit 2 Gerinnefortsätzen (Abb. 1): Barbarossahöhle (nach VÖLKER), Folge großer Hallen, keine nennenswerten Nebengänge): Heimkehle (nach STOLBERG 1926), Folge großer Hallen mit Parallelstrecken und kleineren Seitengängen: GGL = 1780 m, Ausdehnung 700 m x 250 m, GL = 2,5; GF = 18 Hermannshöhle im Harz (nach VÖLKER), verwickeltes Höhlensystem in mehreren Etagen: Segeberger Höhle (nach FRICKE 1989 und GRIPP 1913), labyrinthartige Höhle mit längerem Ostgang; GGL = 1985 m, Ausdehnung 280 m x 125 m, GL = 7,1; GF = 113 Höllern (nach GÖTZ 1979 und briefl. Mitt. S. KEMPE 1996), Netz enger Gänge (Abb. 1): Kluterthöhle (nach GRIEPENBURG 1931), netzartiges Gangsystem: GGL = 5200 m, Ausdehnung 390 m x 190 m; GL = 13; GF = 365 Dachstein-Mammuthöhle (nach HARTMANN 1996), alpine Großhöhle: GGL = 50,1 km; Ausdehnung 2,3 x 1,3 km; GL = 22; GF = 839 Hölloch (nach BÖGLI 1970): sehr verzweigte Großhöhle: GGL = 109 km, Ausdehnung Optimisticeskaja, Ukraine (Stand 1973; pers. Mitt. R. VÖLKER), engmaschiges Labyrinth: GGL = 101,3 km, Ausdehnung 1,8 km x 1,1 km; GL = 56; GF = 5185 Als Extrembeispiele von Grundrißtypen mögen noch folgen: Kammerbacher Höhle (nach STOLBERG 1930): unverzweigter Einzelraum; GGL = 42 m, Ausdehnung 42 m x 25 m; GL = 1; GF = 1,7 Kuxloch an der Helbeburg (nach Stolberg 1935): unverzweigte, enge Klufthöhle: GGL = 25 m, Ausdehnung 25 m x 1 m; GL = 1; GF = 25 Schlußfolgerungen Längenvergleiche sind nur für Höhlen mit ähnlicher Gangdichte sinnvoll. Die Werte für die großräumigen Gipshöhlen im Südharz sind deutlich niedriger als die der labyrinthischen Systeme mit den imponierenden Gesamtganglängen, die sich dadurch allerdings zum Teil relativieren! Die Labyrinthe der Oplimisticeskaja sind in fünf Gruppen zusammengeballt; die Umschreibung des Höhlenareals durch ein Rechteck wird zudem durch einen einzelnen Gang von 400 in Länge verfälscht. Bei anteilsmäßiger Berechnung für die einzelnen Teile und ohne Berücksichtigung des Südganges für das Bezugsdreieck würde sich sogar eine flächenbezogene Gangdichte GF> 7000 ergeben. Die Beispiele Kammerbacher Höhle und Kuxloch zeigen die mangelnde Signifikanz des nur längenbezogenen Wertes für solche Sonderfälle. Aber auch die Barbarossahöhle und die dem gegenüber wesentlich komplizierter angelegte Hermannshöhle unterscheiden sich wesentlich nur im flächenbezogenen Wert, der sich mithin als besser und aussagekräftiger erweist. Trotz, seiner etwas aufwendigeren Bestimmung wäre also die flächenbezogene Gangdichte GF· zur Charakterisierung zu bevorzugen. Letztlich ersetzt auch dieser Kennwert natürlich nicht die Information, die ein noch so primitiver Höhlenplan bietet. Die Festlegung auf eine rechteckige Bezugsfläche ist natürlich ein Notbehelf und kann bei Höhlengrundrissen, welche dieses Rechteck nur zum kleineren Teil wirklich füllen, zu weniger repräsentativen Ergebnissen führen. Eine präzisere Festlegung der umschließenden Fläche wäre denkbar, aber u. U. nicht mehr eindeutig reproduzierbar. Darüber läßt sich diskutieren, ohne das Prinzip der flächenbezogenen Länge grundsätzlich in Frage zu stellen. Die hier nicht weiter diskutierte volumenbezogene Gangdichte GV = GGL³ / (A x B x H) mit ergibt sehr unhandliche Zahlenwerte und wäre ohnehin nur bei Höhlen mit Höhendifferenzen in der Größenordnung der horizontalen Ausdehnung sinnvoll. Bei solchen Höhlen taucht aber erfahrungsgemäß der Gesamthöhenunterschied ohnehin als zusätzliche Information in den Listen auf. Literatur REINBOTH, Fritz (1997): Gesamtganglänge und bezogene Gangdichte - ein Vorschlag zur Verbesserung tabellarischer Längenangaben von Höhlen.- Die Höhle 48:21-25, 1 Abb., Wien |